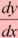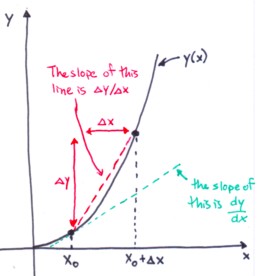
This song rather nicely lays out the mathematical definition of the derivative of a function y(x). Most fundamentally, the derivative of y(x), which is written and pronounced "dy dx", is defined as the slope of the graph of y vs. x. In the figure, at the point x₀, the slope of the curve is equal to the slope of the green line which is tangent to the curve. 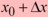We can very roughly approximate this slope by computing the slope of a line drawn between the points on the curve at x₀ (pronounced "x nought") and at (pronounced "x nought plus Delta-x"), as shown by the red line. The slope of this line is the "rise over the run", in other words the slope is 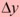(the change in y) divided by 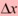(the change in x). If we make 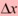smaller and smaller, then 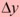also gets smaller, and the slope of the red line gets closer and closer to the slope of the green line. In the ultimate "limit" that 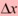becomes infinitesimally small (in the song "send delta-x to zero"), the two slopes are equal.

--WFS 9/1/05

(Click to enlarge)