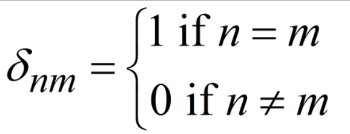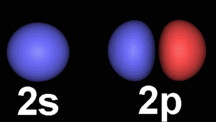
The Physics of the Kronecker Delta Function Song

The "quantum" in quantum mechanics originates from the peculiar fact that, when you measure the energy of an electron in an atom, you only find certain well defined values, and never anything in between. (These are the 1s, 2s, 2p, etc. levels you may have heard of.) One can show mathematically that the corresponding quantum states are "perpendicular" to each other !!

To understand what this means, we need the following definition of perpendicularity:

Say we are checking for perpendicularity between state 1 and state 2, each of which is represented by a "wave function" that takes on different values for each point in space. We divide space into infinitesimally small cubes. For each cube, we multiply the value of wave function 1 times the value of wave function 2. We then add together add these multiplication results for all the cubes. This is called taking the "inner product" of the two wave functions. (It's like a dot product for vectors.)

If the two states are perpendicular, their inner product is zero. You can see this qualitatively for the 2s and 2p states of a hydrogen atom, which are shown here:

(Image by Dr. Alex Clark, Chemical Computing Group, Inc.)

The 2s wavefunction is positive everywhere, as indicated by the blue color. The 2p is positive on the left (blue) and negative on the right (red). So, when you multiply them together for cubes on the left, the result is positive, while for cubes on the right the result is negative. Then, when you add up all the multiplication results, you get zero, so 2s and 2p are "perpendicular".

On the other hand, if we did the same operation not on two different states, but on two copies of the same state, e.g. 2p and 2p, the result of each multiplication is positive everywhere. It turns out that when you add up all the multiplication results, you simply get 1 !

To use the Kronecker Delta Function, we just number all the states using integers. For example, we could assign the number 1 to 1s, 2 to 2s, 3 to 2p, etc. If we take the inner product of states with two different numbers, say n = 1 and m = 2, we get zero. However, if we take the inner product of two copies of the same state, say n = 2 and m = 2, we get 1. That's what the Kronecker Delta Function says:

Return to main Kronecker Delta Function Song page .. Return to PhysicsSongs.org main page

Background image: Artist's conception of Hilbert Space, the special space in which quantum states are represented as vectors. ID 106200085 © Mast3r | Dreamstime.com